Ben Schneider’s Blog – Practical Significance

Some Options for Fast Matrix Decompositions in R

R

Rust

Math

This short post shows some different options for speeding up matrix decompositions in R, which can speed up a wide variety of commmon statistical functions.

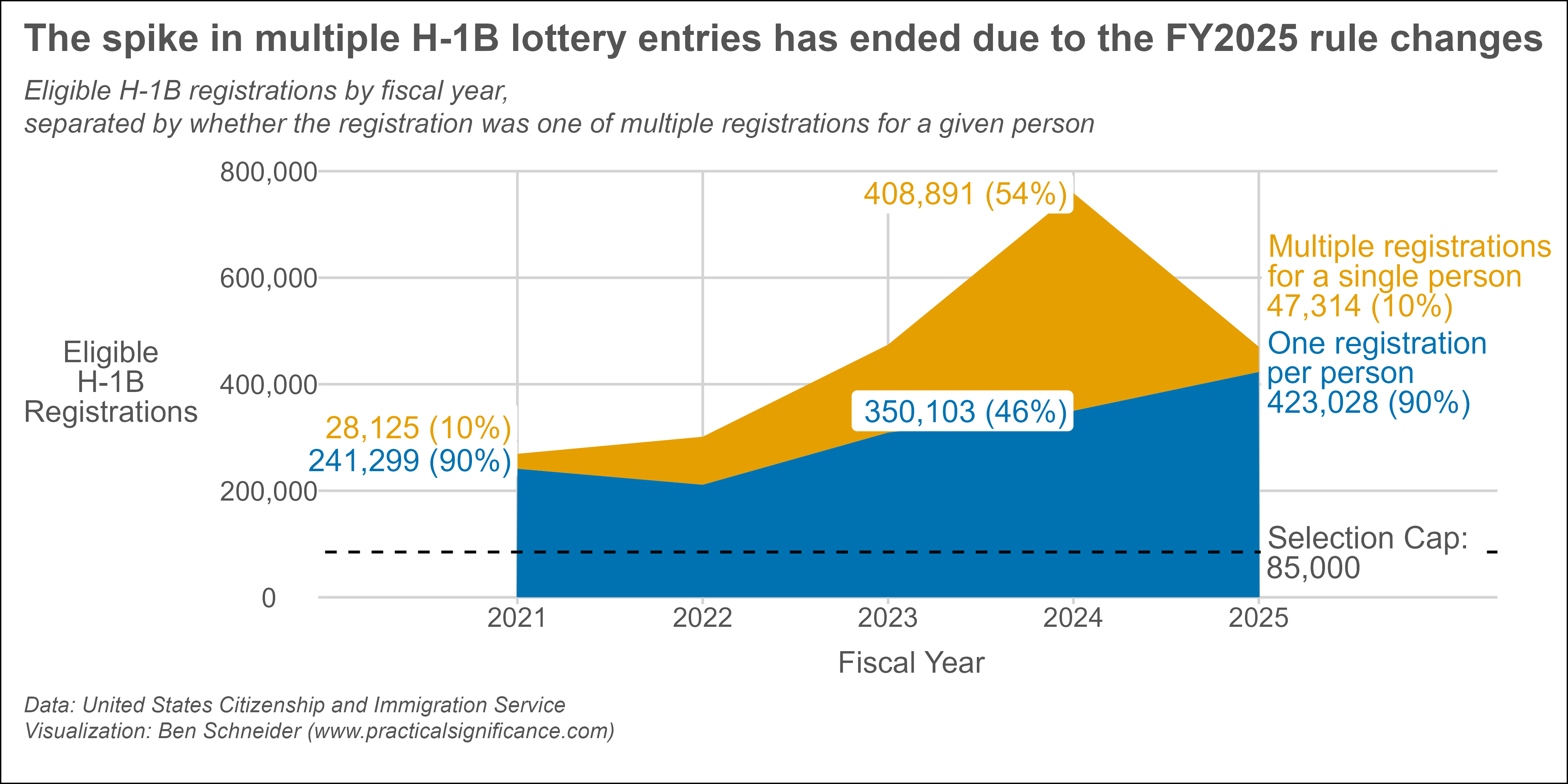
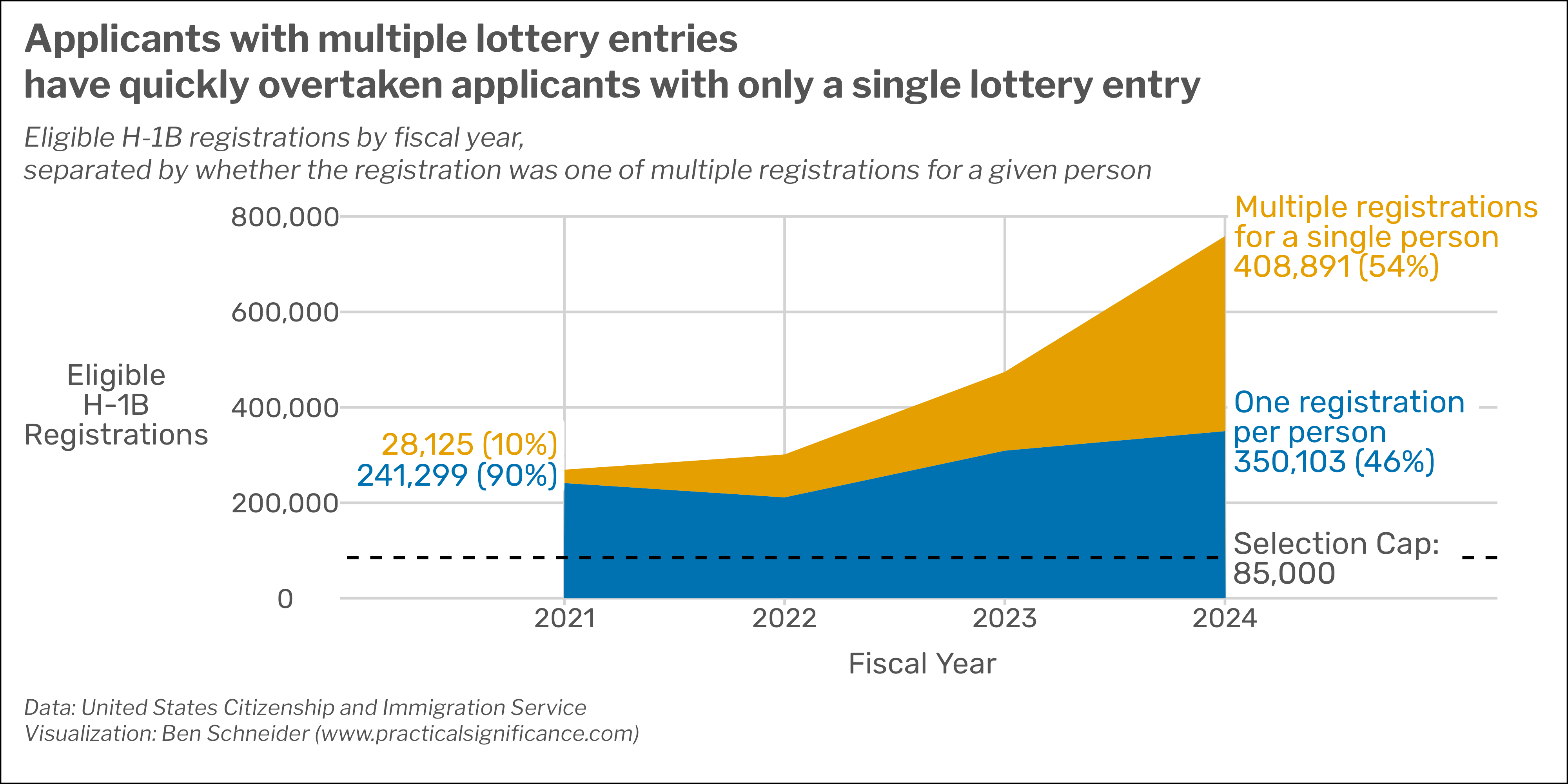
Visualizing the H-1B Fraud Spike and the Impact of Lottery Rule Changes

miscellaneous

visualization

This year’s change in H-1B lottery rules put an end to the spike in companies submitting multiple fraudulent lottery entries for individual applicants. This post visualizes the stark pattern in the published data from USCIS.

Simulation-based Variance Estimation for the Cube Method

sampling

surveys

R

Julia

This post shows a couple approaches for using simulation to help improve variance estimation for samples selected using the cube method. It also proposes a new variance estimator that combines the strengths of existing variance estimators to potentially yield more reliable variance estimates for the cube method.

Balanced sampling in R, Julia, and R + Julia

sampling

surveys

R

Julia

This post shows a small case study of developing code for a statistical sampling algorithm side-by-side in R and Julia.

Hanukkah of Data 5784: R and Julia

R

Julia

Hanukkah-of-Data

This post documents my experience using R and Julia to solve this year’s Hanukkah of Data challenges.

Stacking Replicate Weights

statistics

surveys

R

This short post explains what we’re really doing when we stack replicate weights from different surveys.

Multiway Stratification Using Cube Sampling

sampling

statistics

R

Cube sampling provides a useful generalization of several sampling methods, including stratified sampling. This post demonstrates how we can use cube sampling to accomplish the goals we often have when using stratified sampling.

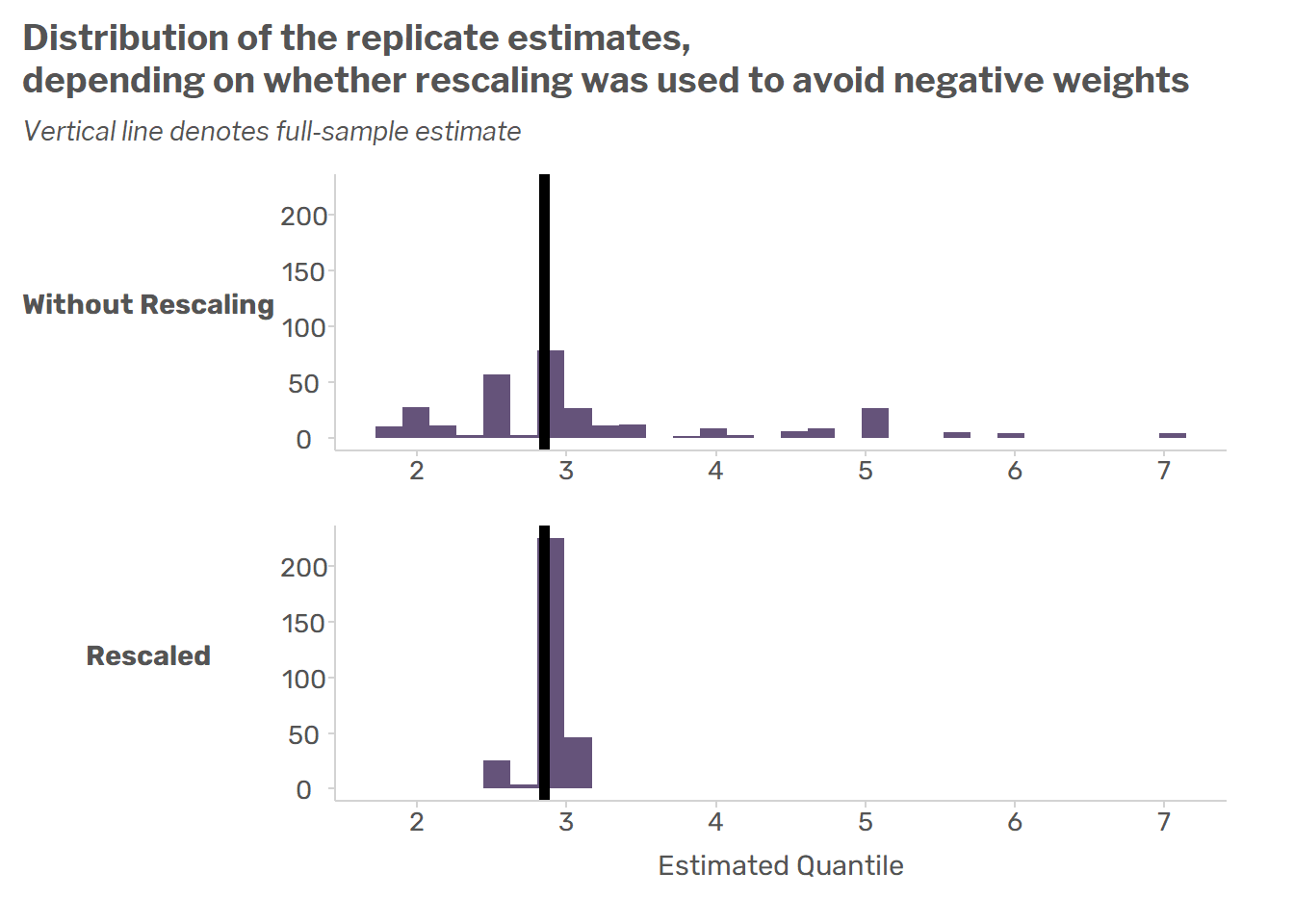
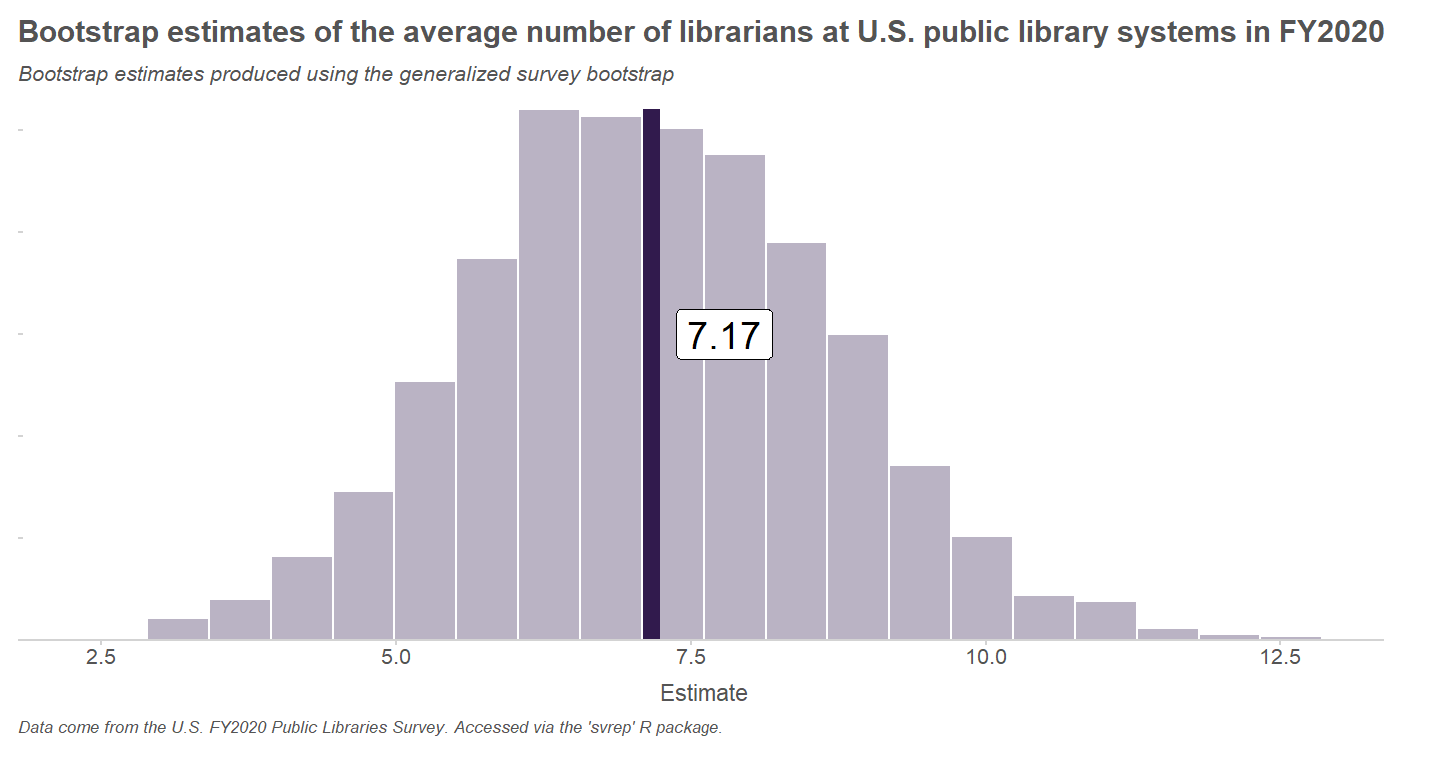
Avoiding Negative Weights in the Generalized Bootstrap

sampling

statistics

R

The generalized bootstrap is a promising tool for survey data, but one of the key challenges with it in practice is that it can generate negative replicate weights. This post describes the challenges posed by negative weights and demonstrates an overlooked problem with the main solutions proposed to deal with it.

An Optimization-based Bootstrap

sampling

statistics

R

Creating bootstrap weights for survey data can be viewed as a constrained optimization problem: obtain low-error variance estimates with as few replicates as possible using nonnegative weights. The standard solution to this problem is to use an effective but inefficent random resampling method. But what if we tried using an optimization algorithm?

Visualizing the H-1B Boom

miscellaneous

visualization

Recent articles on the huge increase in H-1B registrations have included a lot of numbers but no visualization. This post provides some much-needed visualization.

Bootstrapping all the things

The new version of the ‘svrep’ package on CRAN helps you implement bootstrap methods for surveys, even those with particularly complex sample designs.

Nonresponse weighting class adjustments are model predictions

statistics

surveys

R

A short post explaining how nonresponse weighting class adjustments can be interpreted as model predictions. Includes a little bit of math and a little bit of R.

More on Speeding up the Survey Package: Adding the New C++ Functions to the Package

statistics

surveys

R

survey package

Following up on an earlier post about speeding up the {survey} package using {Rcpp} and {RcppArmadillo}, I show how the new, faster functions can be incorporated into the package along with accompanying unit tests. I also show how the speed of the original base R functions and the {Rcpp} versions scale as survey designs increase in size.

How are R and Stata (mis)handling singleton strata?

statistics

surveys

R

Stata

software

Analysts attempting to estimate variance contributions from “singleton strata” often use the “adjust”/“recentering” options implemented in R and Stata, whose meaning is unclear due to ambiguous documentation. In this post, I try to clarify what these options are actually doing in theory, and I show that in practice their software implementations have surprising bugs.

Calculating R Indicators in R

statistics

surveys

R

A short post on calculating R indicators (and their sampling variance) in R.

Fitting a basic Fay-Herriot model in Stan and JAGS

statistics

bayes

MCMC

Stan

JAGS

A short post showing how to fit a very basic, Bayesian Fay-Herriot model in Stan and JAGS. This post focuses on model specification, fitting, and visualization.

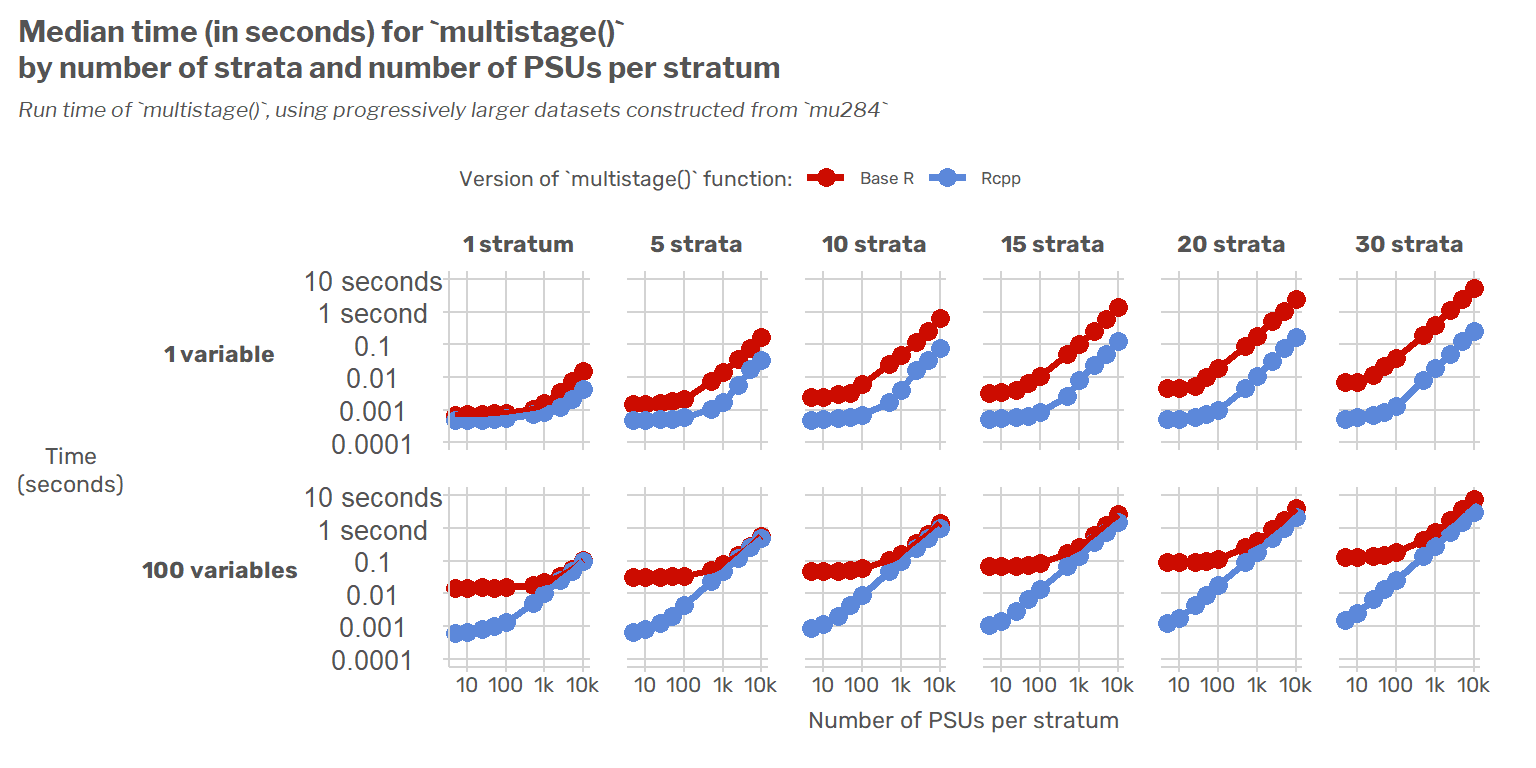
Making the {survey} package hundreds of times faster using {Rcpp}

statistics

surveys

R

survey package

A common objection to using the {survey} package instead of SAS or Stata is the computational time it requires. In this post, I show that we can easily obtain hundred-fold speed improvements in its core functions by using the {Rcpp} and {RcppArmadillo} packages. To illustrate, I show how we can make svytotal() run over 500 times faster. Finally, I offer thoughts about how to incorporate these {Rcpp}-based functions in either the {survey} package or a potential add-on R package.

Understanding the code used to implement the {survey} package’s recursive variance estimation for multistage samples

statistics

surveys

R

survey package

Unlike SAS and SPSS, the {survey} package in R can properly estimate variances for designs with multistage sampling and significant sampling fractions. The estimation is implemented using a recursive algorithm, whose basic idea is well-documented but whose R code is a bit intimidating to understand. This post walks through the R code used to implement this algorithm.

What’s the margin of error for the employee engagement index?

employee engagement

statistics

surveys

sampling

R

The key performance metric of many employee engagement surveys, the Engagement Index, is a statistic whose margin of error is deceptively difficult to estimate. As a result, many organizations fail to present a margin of error at all. I discuss why this estimation problem is difficult using the standard tools of engagement researchers, and I suggest two solutions based on tools from survey sampling theory. I provide example R code and discuss how to estimate the margin of error in general-purpose, non-statistical software.

Establishing the influence function method’s asymptotic validity

math

statistics

surveys

sampling

A math-heavy post giving a background and detailed proof of the theorem used to justify the method of linearization based on influence functions for sample surveys.

Systematic sampling as implicit stratification

statistics

surveys

sampling

This short post illustrates why systematic sampling is sometimes referred to as ‘implicit stratification’.

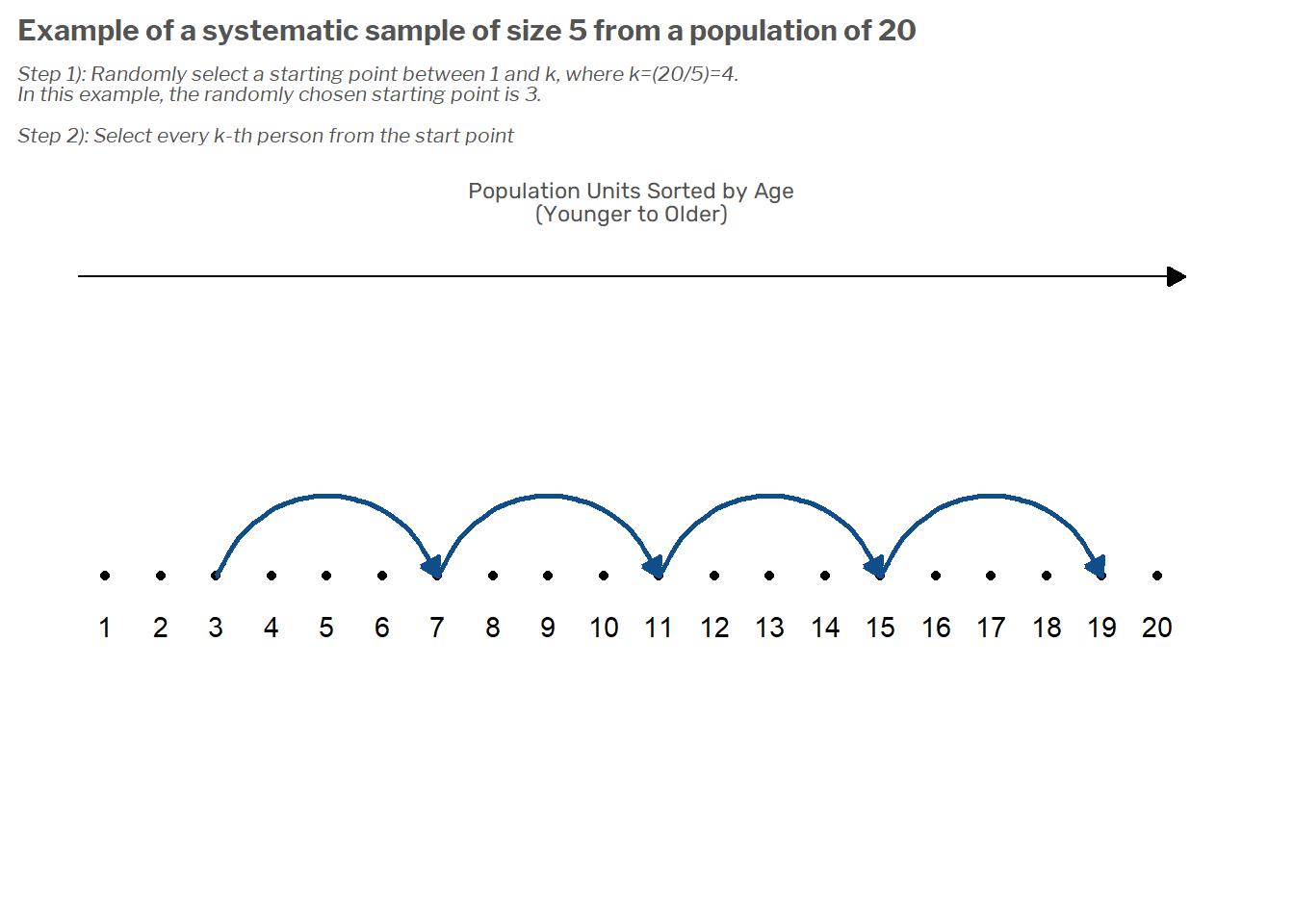
How correlated are survey estimates from overlapping groups?

statistics

surveys

sampling

simulation

R

We examine one approach for estimating the correlation of survey estimates from overlapping groups, such as 30-50 year olds and 40-60 year olds, using the method of linearization by influence functions. I provide a walk-through in R and use simulations to evaluate the method’s performance.

How is the survey R package estimating covariances between domain estimates?

statistics

surveys

An example and an explanation of the package’s new method of using influence functions to estimate covariances

Reflections on deciding to leave for grad school

personal

JPSM

mentoring

Reflecting on my decision to leave IQS and Louisville

What we estimate when we estimate regression models with survey data

statistics

regression

surveys

sampling

I explain the reasoning behind why survey software estimates regression parameters and their standard errors the way it does.